Question

How do you solve this math problem: cloee brought $50.75 to the state fair. She brought a burger, a souvenir and a pass. The burger was 1/6 as much as the souvenir, and the souvenir cost 3/4 the cost of the pass. Chloe had $2.00 left over after buying these items.

Answer 1

The souvenir cost $19.50

The burger cost $3.25

The pass cost $26

Explanation:

System of Equations

There are three unknowns in the problem. We must find how much did Chloe spend in the burger, the souvenir, and the pass. The data provided is

She spent %50.75-$2=$48.75 on the three items.

The burger was 1/6 as much as the souvenir

The souvenir was 3/4 the cost of the pass.

Let's call b, s, and p to the cost of the burger, souvenir, and pass respectively. The conditions of the problem can be written as

b+s+p= 48.45

`b=(1/6)s`

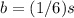
s=(3/4)p

The last equation allows us to solve for p:

p=(4/3)s

Now we substitute in the first equation

(1/6)s+s+(4/3)s=48.75

Operating

2.5s=48.75

Solving

s=48.75/2.5=19.50

The souvenir cost $19.50

Now

b=(1/6)s=(1/6)(19.50)=3.25

The burger cost $3.25

And finally

p=(4/3)s=(4/3)(19.50)=26

The pass cost $26

Summary:

The souvenir cost $19.50

The burger cost $3.25

The pass cost $26