Question

Chromium-51 has a half life of 27.70 days. How much will be left after 166.2 days if

you started with a 924 gram sample? How much decayed?

O

14.44g left; 909.56g decayed

35.54g left; 888.46g decayed

'all of it decayed

14.44g left; 938.44g decayed

Answer 1

Decayed mass: 909.56 g, Left mass: 14.44 g.

Step-by-step explanation:

The time constant of the Chromium-51 is:

`\tau = (t_(1/2))/(\ln 2)`

`\tau = (27.70\,days)/(\ln 2)`

`\tau = 39.963\,days`

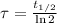
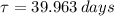
The decay equation for the isotope has the following form:

`(m(t))/(m_(o)) = e^{-(t)/(\tau) }`

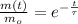
The total decay at a given instant t is:

`\% \delta = \left(1-e^{-(t)/(\tau) } \right) * 100\,\%`

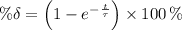
The total decay at 166.2 days is:

`\% \delta = 98.437\,\%`

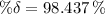
Decayed mass: 909.56 g, Left mass: 14.44 g.