Question

two cars travel at same speed to different destinations. car A reaches its destination in 24 minutes. car B reaches its destination in 32 minutes. Car B travels 5 miles farther than car A. How fast do the cars travel?​

Answer 1

The speeds of the cars is: 0.625 miles/minute

Explanation:

We use systems of equations in two variables to solve this problem.

Recall that the definition of speed (v) is the quotient of the distance traveled divided the time it took :
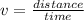`v=(distance)/(time)`. Notice as well that the speed of both cars is the same, but their times are different because they covered different distances. So if we find the distances they covered, we can easily find what their speed was.

Writing the velocity equation for car A (which reached its destination in 24 minutes) is:

`v\,*\,24\,min=d_A`

Now we write a similar equation for car B which travels 5 miles further than car A and does it in 32 minutes:

`v\,*\,32\,min=d_A+5\,miles`

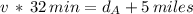
Now we solve for
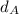`d_A` in this last equation and make the substitution in the equation for car A:

`v\,*\,32\,min=d_A+5\,miles\\d_A=v\,*\,32\,min-5\,miles\\\\v\,*\,24\,min=v\,*\,32\,min-5\,miles\\v\,(24\,min-32\,min)=-5\,miles\\v\,(-8\,min)=-5\, miles\\v=(-5)/(-8) (miles)/(min) \\v=0.625\,(miles)/(min)`

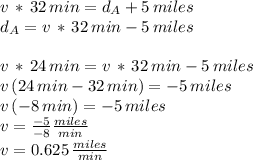
So this is the speed of both cars: 0.625 miles/minute