Answer:
The average number of customers in the system is 3.2
Explanation:
The average number of customes in the system is given by:
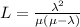
In which
 is the number of arirvals per time period
is the number of arirvals per time period
 is the average number of people being served per period.
is the average number of people being served per period.
The number of arrivals is modeled by the Poisson distribution, while the service time is modeled by the exponential distribution.
Customers arrive at the stand at the rate of 28 per hour
This means that
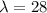
Service times are exponentially distributed with a service rate of 35 customers per hour.
This means that
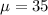 . So
. So
The average number of customers in the system (i.e., waiting and being served) is
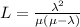
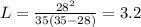
The average number of customers in the system is 3.2