Answer:
Explanation:
I think your question is missed of key information, allow me to add in and hope it will fit the original one.
Consider f(x) =
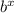 . Which statement(s) are true for 0 < b < 1? Check all that apply.
. Which statement(s) are true for 0 < b < 1? Check all that apply.
The domain is all real numbers.
The domain is x > 0.
The range is all real numbers.
The range is y > 0.
The graph has x-intercept 1.
The graph has a y-intercept of 1.
The function is always increasing.
The function is always decreasing.
My answer:
The domain is all real numbers.
True, the domain of a function is the complete set of possible values of the independent variable. Here, we can have unlimited values of x so we will have unlimited values of f(x)
<=> our domain (0 , +∞ )
The domain is x > 0.
Wrong, as we discussed in the aforementioned answer.
The range is all real numbers.
Wrong
The range is y > 0.
True, the range of a function is the complete set of all possible resulting values of the dependent variable (f(x), usually), after we have substituted the domain. Because this is an exponential function so:
<=> our range (0 , +∞ ) or y>0
The graph has x-intercept 1.
we can set f(x)=0 and then we can solve for x
f(x) =
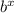 = 0
= 0
x is undefined so, x-intercept does not exist
The graph has a y-intercept of 1
y-intercept when x is 0, so f(x) = 1 . True.
The function is always decreasing
Because 0 < b < 1, The function is always decreasing when we increase the value of x.
So we choose A D F H