Question

Ethanoic acid has a pKa of 4.75. Find the pH of the solutions that results from the addition of 40.0 mL of 0.040 M NaOH to 50.0 mL of 0.075 M ethanoic acid.

Answer 1

About 4.63.

Step-by-step explanation:

The reaction between ethanoic acid (CH₃COOH) and sodium hydroxide (NaOH) can be described by the following net ionic equation:

`\displaystyle \text{CH$_3$COOH}_\text{(aq)} + \text{OH}^-_\text{(aq)}\longrightarrow \text{CH$_3$COO}^-_\text{(aq)} + \text{H$_2$O}_\text{($\ell$)}`

40.0 mL of 0.040 M NaOH contains:

`\displaystyle 40.0\text{ mL} \cdot \frac{0.040\text{ mol NaOH}}{1000\text{ mL}} = 0.0016\text{ mol NaOH}`

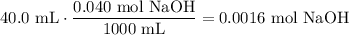
Because NaOH is a strong base, it dissociates completely. Hence, the amount of OH⁻ present is 0.0016 mol. Na⁺ acts as a spectator ion.

50.0 mL of 0.075 M CH₃COOH contains:

`\displaystyle 50.0\text{ mL} \cdot \frac{0.075\text{ mol CH$_3$COOH}}{1000\text{ mL}} = 0.0038\text{ mol CH$_3$COOH}`

OH⁻ is the limiting reagent of the reaction. Therefore, as the reaction proceeds to completion:

• The amount of OH⁻ drops to 0 mol.

• The amount of CH₃COOH decreases to (0.0038 - 0.0016) mol = 0.0022 mol.

• And the amount of CH₃COO⁻ increases to (0 + 0.0016) mol = 0.0016 mol.

Note that all species present are in a one-to-one ratio.

To find pH, we can use the Henderson-Hasselbalch equation:

`\displaystyle \text{pH} = \text{p}K_a + \log\frac{[\text{Base}]}{[\text{Acid}]}`

The total volume of the solution is 40.0 mL + 50.0 mL = 90.0 mL.

Hence, find [CH₃COOH]:

`\displaystyle \left[\text{CH$_3$COOH}\right] = \frac{0.0022\text{ mol}}{90.0\text{ mL}} \cdot \frac{1000\text{ mL}}{1\text{ L}} = 0.024\text{ L}`

Find [CH₃COO⁻]:

`\displaystyle \left[\text{CH$_3$COO}^-\right] = \frac{0.0016\text{ mol}}{90.0\text{ mL}}\cdot \frac{1000\text{ mL}}{1\text{ L}} = 0.018\text{ M}`

Therefore, the pH of the resulting solution is:

`\displaystyle \begin{aligned}\text{pH} & = \text{p}K_a + \log\frac{[\text{Base}]}{[\text{Acid}]} \\ \\ & = (4.75) + \log ((0.018))/((0.024)) \\ \\ & = 4.75 + (-0.12) \\ \\ & = 4.63\end{aligned}`

In conclusion, the pH of the resulting solution is about 4.63.