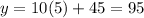Answer:
Part 1) Option B.
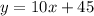
Part 2) The score is 95
Explanation:
Part 1) Linear equation that best describes the given model
Let
x ---> number of hours students spent studying
y ---> their score on the test
Looking at the line that was fit to the data to model the relationship
The slope is positive
The y-intercept is the point (0,45)
For x=1, y=55 ----> point (1,55)
Find the slope
The formula to calculate the slope between two points is equal to
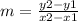
substitute the points (0,45) and (1,55)
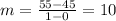
Find the equation of the line in slope intercept form
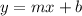
we have
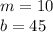
substitute
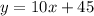
Part 2) Estimate the score for a student that spent 5 hours studying.
For x=5 hours
substitute in the linear equation and solve for y