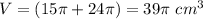Question

Consider this composite figure.

2 cones. The top cone has a height of 5 centimeters and radius of 3 centimeters. The bottom cone has a height of 8 centimeters and radius of 3 centimeters.

Apply the formula of each shape to determine the volumes.



What is the exact volume of the composite figure?

Answer 1

`V=39\pi\ cm^3`

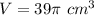
Explanation:

we know that

The volume of a cone is given by the formula

`V=(1)/(3)\pi r^(2) h`

where

r is the radius of the circular base of cone

h is the height of the cone

step 1

Find the volume of the top cone

we have

`r=3\ cm\\h=5\ cm`

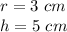
substitute

`V=(1)/(3)\pi (3)^(2) (5)`

`V=15\pi\ cm^3`

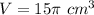
step 2

Find the volume of the bottom cone

we have

`r=3\ cm\\h=8\ cm`

substitute

`V=(1)/(3)\pi (3)^(2) (8)`

`V=24\pi\ cm^3`

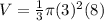
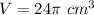
step 3

Find the exact volume of the composite figure

Adds the volume of the top cone plus the volume of the bottom cone

`V=(15\pi+24\pi)=39\pi\ cm^3`