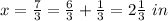Question

In circle E shown, points C, E, and D lie on a straight line. The length of CD is 36 inches. If

the length of EF is given by 3x +11 then which of the following is the value of x?

Answer 1

`x=2(1)/(3)\ in`

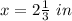
Explanation:

we know that

In the given circle, the segment CD is a diameter (because is a chord that passes through the center E)

The given diameter is
`D=36\ in`

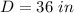
The radius of the circle is half the diameter

so

`r=36/2=18\ in`

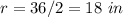
we have

`EF=3x+11`

Remember that the distance from the center to any point on the circle is equal to the radius of the circle

so

The length of segment EF is equal to the radius

`3x+11=18`

solve for x

`3x=18-11\\3x=7\\x=(7)/(3)\ in`

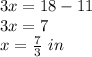
Convert to mixed number

`x=(7)/(3)=(6)/(3)+(1)/(3)=2(1)/(3)\ in`