Question

Convert r = 8cos θ to rectangular form.

Answer 1

`(x-4)^2+y^2=16`

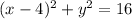
This is a circle with radius
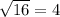`√(16)=4` and center
`(4,0)`.

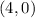Explanation:

Recall the following:

`x=r\cos(\theta)`

`y=r\sin(\theta)`

`(y)/(x)=\tan(\theta)`

`x^2+y^2=r^2`

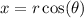
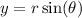
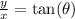
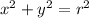
We are given
`r=8\cos(theta)`.

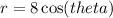Multiply both sides by
`r`:

`r(r)=8\cos(\theta)r`

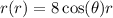
Reorder on right and simplify on left:

`r^2=8r\cos(theta)`

We can now make some replacements from our "Recall" section:

`x^2+y^2=8x`

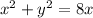
We can probably leave like this, but sometimes we are required to put in a more identifying form.

This is a circle. I'm going to write in the form
`(x-h)^2+(y-k)^2=r^2`.

Subtract
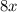`8x` on both sides:

`x^2-8x+y^2=0`

`x^2-8x+\text{(blank)}+y^2=0+\text{(blank)}`

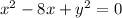
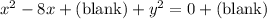
We are going to fill those "blanks" in so that we can complete the square for the
`x` part.

`x^2-8x+((-8)/(2))^2+y^2=0+((-8)/(2))^2`

`(x+(-8)/(2))^2+y^2=0+(-4)^2`

`(x-4)^2+y^2=0+16`

`(x-4)^2+y^2=16`

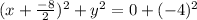
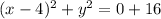
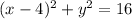
So our equation is that of a circle with radius
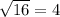`√(16)=4` and center
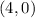`(4,0)`.