Question

On a coordinate plane, triangle A B C is shown. Point A is at (3, 4), point B is at (negative 5, negative 2), and point C is at (5, negative 2). In the diagram, AB = 10 and AC = 2 StartRoot 10 EndRoot. What is the perimeter of △ABC? 10 units 10 + 2 StartRoot 10 EndRoot units 20 units 20 + 2 StartRoot 10 EndRoot units

Answer 1

The perimeter of Δ ABC is 20 + 2
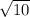`√(10)` units ⇒ Last answer

Explanation:

The perimeter of any triangle is the sum of the lengths of its three sides

The formula of distance between two points is
`d=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`

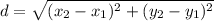
In Δ ABC

∵ A = (3 , 4) , B = (-5 , -2) , C = (5 , -2)

∵ AB = 10 units

∵ AC = 2
`√(10)`

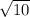
- To find its perimeter find the length of BC

∵
`x_(1)` = -5 and
`y_(1)` = -2

∵
`x_(2)` = 5 and
`y_(2)` = -2

- By using the formula above

∴
`BC=\sqrt{(5--5)^(2)+(-2--2)^(2)}=\sqrt{(5+5)^(2)+(-2+2)^(2)}`

∴
`BC=\sqrt{(10)^(2)+(0)^(2)}=√(100)`

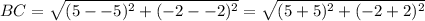
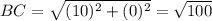
∴ BC = 10 units

To find the perimeter add the lengths of the three sides

∵ P = AB + BC + AC

∴ P = 10 + 10 + 2
`√(10)`

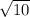
- Add like terms

∴ P = 20 + 2
`√(10)`

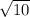
The perimeter of Δ ABC is 20 + 2
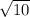`√(10)` units