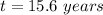Answer:
Explanation:
we know that
The compound interest formula is equal to
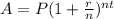
where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest in decimal
t is Number of Time Periods
n is the number of times interest is compounded per year
in this problem we have
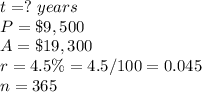
substitute in the formula above
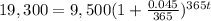
solve for t
simplify
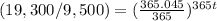
Apply log both sides
![log(19,300/9,500)=log[((365.045)/(365))^(365t)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/k2iw17jxjjfv34u6vsywq0nzo2d1zpcsjp.png)
Apply property of logarithms in the right side
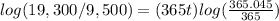
![t=log(19,300/9,500)/[(365)log((365.045)/(365))]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/pvvvkuzfk3z90rxj752s97tkmb6s1cn3qg.png)