Question

a map of barn is shown in coordinate plane in which the coordinates are measured in yards. The map shows the barn a (4,6). A well is dug at (4, y). What are the two values of y such that the barn is 70 yards from the well

Answer 1

The values of y such that the barn is 70 yards from the well are y=76 or y=-64

Explanation:

Distance in the Plane

Given two points in a rectangular system of coordinates (a,b) and (c,d) the distance measured between them is calculated with the formula

`d=√((c-a)^2+(d-b)^2)`

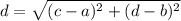
The barn is located at (4,6) and the well is located at (4,y). The value of y must be calculated in such a way the distance between the barn and the well is 70 yards. Thus, the equation to solve is

`70=√((4-4)^2+(y-6)^2)`

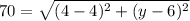
Operating

`70=√((y-6)^2)`

When taking the square root we must be careful for it has two signs:

`70=\pm (y-6)`

Rearranging

`y-6=\pm 70`

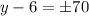
which yields to these solutions

`y-6=70`

`\boxed{y=76}`

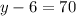
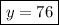
And also

`y-6=-70`

`\boxed{y=-64}`

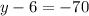
The values of y such that the barn is 70 yards from the well are y=76 yards or y=-64 yards