Question

Solve the equation by factoring
`x^(3) -16x^(2) } +63x=0`

Answer 1

x = 0, or x = 7, or x= 9

Explanation:

Start by extracting all common factors of the polynomial expression on the left (in our case the only common factor to all terms is "x"):

`x^3-16x^2+63x=0\\x(x^2-16x+63)=0`

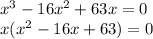
Now, let's focus on writing the trinomial in parentheses in factor form by finding two integer numbers whose product is 63, and that combined give -16.

The pair of two numbers that satisfy these requirements are: -7, and -9

Let's use them to split the term in "x" (the linear term of the trinomial), and then use factoring by grouping to completely factor the trinomial:

`x^2-16x+63\\x^2-9x-7x+63\\(x^2-9x)+(-7x+63)\\x(x-9)-7(x-9)\\(x-9)(x-7)`

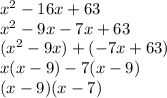
So now we use these two factors in the original equation to replace the quadratic trinomial :

`x\,(x^2-16x+63)=0\\x(x-9)(x-7)=0`

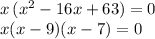
In order for a product of these three factors to give zero, we need at least one of them to be zero. That is:

x = 0, or x = 7, or x= 9

Therefore these three values are solutions to the original equation.