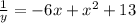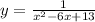Question

What’s the differential equation of

dy/dx = y^2 (6-2x)


With initial condition that when x=3, y=1/4

Answer 1

`y=(1)/(x^(2)-6x+13 )`

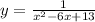
Explanation:

We have given,

`(dy)/(dx)=y^(2)(6-2x)`

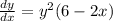
and initial condition
`x=3,\ y=(1)/(4)`

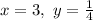
Now,

`(dy)/(dx)=y^(2)(6-2x)`

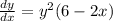
Rearranging the variables, we get

`(dy)/(y^(2) )=(6-2x).dx`

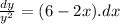
Applying integration both sides, we get

`\int\ {(dy)/(y^(2) ) } \,=\int\ {(6-2x).} \, dx`

⇒
`(-1)/(y) =6x-(2x^(2) )/(2)`

⇒
`(-1)/(y)=6x-x^(2) +C`

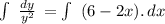
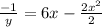
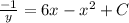
Putting the initial condition (i.e.,
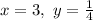`x=3,\ y=(1)/(4)`), we get

⇒
`-4=6*3-(3)^(2)+C`

⇒
`-4=18-9+C`

∴
`C=-13`

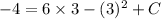
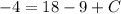
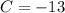
We have,
`(-1)/(y)=6x-x^(2) +C`

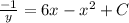
now putting the value of
`C` in above equation, we get

⇒
`(-1)/(y)=6x-x^(2) -13`

⇒
`(1)/(y)=-6x+x^(2) +13`

`y=(1)/(x^(2)-6x+13 )`