Question

A cylinder has diameter of 4ft and a height of 9ft. Explain whether halving the diameter has the same effect on the surface area as halving the height.

Answer 1

See Below

Explanation:

The surface area of cylinder is given by the formula:

`SA=2\pi r^2 + 2\pi r h`

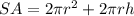
Where

r is radius ( diameter is 4, so radius is 4/2 = 2)

h is height ( h = 9)

Lets find original surface are:

`SA=2\pi r^2 + 2\pi r h\\SA=2\pi (2)^2 + 2\pi (2) (9)\\SA=8\pi +36\pi\\SA=44\pi`

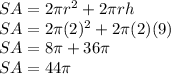
Halving diameter:

diameter would be 4/2 = 2, so radius would be 2/2 = 1

So, SA would be:

`SA=2\pi r^2 + 2\pi r h\\SA=2\pi (1)^2 + 2\pi (1) (9)\\SA=2\pi +18\pi\\SA=20\pi`

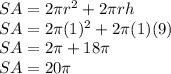
Halving height:

Height is 9, halving would make it 9/2 = 4.5

Now, calculating new SA:

`SA=2\pi r^2 + 2\pi r h\\SA=2\pi (2)^2 + 2\pi (2) (4.5)\\SA=8\pi + 18\pi\\SA= 26\pi`

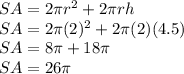
Original SA is
`44\pi`,

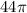Halving diameter makes it
`20\pi`

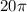
Halving height makes it
`26\pi`

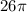
So, halving diameter does not have same effect as halving height.