Question

Franks credit card has no annual fee, 23.99% interest rate. Switch to new card 16.99% rate. $35 annual fee. How much average balance would frank have to make switching cards worth it?

Answer 1

The minimum average balance that makes the switching worth it is $500

Explanation:

Equations

We know Frank's credit card has no annual fees and charges an interest rate of 23.99% of his average balance B. He wants to switch to a new card with $35 annual fees but less interest rate of 16.99%.

The total annual payment Frank actually has to pay is given only by the interest of his annual average balance. That is

`P_1=23.99\%\cdot B=0.2399\cdot B`

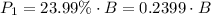
With the new card, he'll have to pay a fixed fee of $35 plus the annual interest:

`P_2=35+16.99\%\cdot B=35+0.1699\cdot B`

To make switching cards worth it, both payments will need to be (at least) equal:

`0.2399\cdot B=35+0.1699\cdot B`

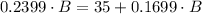
Rearranging

`0.2399\cdot B-0.1699\cdot B=35`

`0.07B=35`

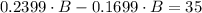
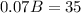
Solving

`B=35/0.07=500`

`B=\$500`

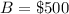
The minimum average balance that makes the switching worth it is $500. If his balance is more than $500, he'll save by using the new card.