Question

A ball is thrown vertically upward from the top of a building 160 feet tall with an initial velocity of 48 feet per second. The distance d (in feet) of the ball from the ground after t seconds is d(t) = 160 + 48t - 16t^2.

After how many seconds does the ball strike the ground? Please explain if you can!
When will the ball reach its maximum height? What is the maximum height of the ball? Please explain if you can!

Answer 1

# after 5 seconds, the ball strikes the ground

# The ball reaches maximum height at t = 1.5 seconds

# The max height is 196 feet

Explanation:

The equation is:

`d(t)=-16t^2+48t+160`

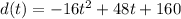
t is the time

d(t) is the distance traveled

Initial height is 160 feet and initial velocity is 48 ft/sec

If we want to find the time it takes the ball to hit the ground, we let d(t) equal to 0 and find t. Shown below:

`-16t^2+48t+160=0\\t^2-3t-10=0\\(t-5)(t+2)=0\\t=5,-2`

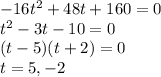
We disregard t = -2 since time can't be negative. We take t = 5

Thus, after 5 seconds, the ball strikes the ground.

The equation is a quadratic of the form:
`ax^2+bx+c`

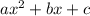
Matching equations, we can say:

a = -16

b = 48

c = 160

The time when ball reaches max height is given as:

`t=-(b)/(2a)`

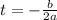
Substituting, we find:

`t=-(b)/(2a)\\t=-(48)/(2(-16))\\t=1.5`

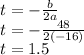
The ball reaches maximum height at t = 1.5 seconds

The max height can be found by putting t = 1.5 into the original equation. Shown below:

`d(t)=-16t^2+48t+160\\d(1.5)=-16(1.5)^2+48(1.5)+160\\=196`

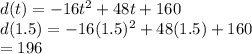
The max height is 196 feet