Answer:
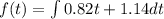
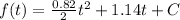
Where C is a constant, now using the initial condition we got:
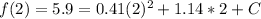
And solving for C we got:
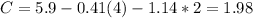
And the function desired for the advertising revenue would be given by:
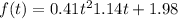
With f the amount in billions and the the years since 2002 to 2006.
Step-by-step explanation:
For this case we have the following function who represent the revenue grew rate:
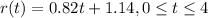
And we want to calculate the Advertising revenue so we need to integrate the function r(t) and we can use the inidital condition t=0 , f(2)= 5.9 billion.
If we integrate the function we got:
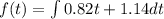
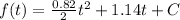
Where C is a constant, now using the initial condition we got:
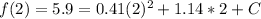
And solving for C we got:
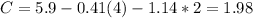
And the function desired for the advertising revenue would be given by:
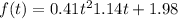
With f the amount in billions and the the years since 2002 to 2006.