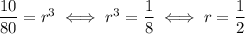In a geometric sequence, consecutive terms have a common ratio:
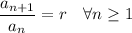
This means that, in order to build a gometric sequence, we must choose an initial value
 and a common ratio
and a common ratio
 , and we'll multiply each term by
, and we'll multiply each term by
 to get the next one:
to get the next one:
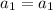
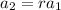
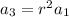
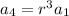
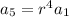
This implies that
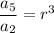
And so in this case we have