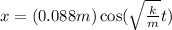Question

What is the equation describing the motion of a mass on the end of a spring which is stretched 8.8 cm from equilibrium and then released from rest

Answer 1

`x=(0.088m)\cos(\sqrt{(k)/(m) } t)`

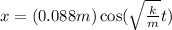
Step-by-step explanation:

We first identify the elements of this simple harmonic motion:

The amplitude A is 8.8cm, because it's the maximum distance the mass can go away from the equilibrium point. In meters, it is equivalent to 0.088m.

The angular frequency ω can be calculated with the formula:

`\omega =\sqrt{(k)/(m)}`

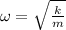
Where k is the spring constant and m is the mass of the particle.

Now, since the spring starts stretched at its maximum, the appropriate function to use is the positive cosine in the equation of simple harmonic motion:

`x=A\cos(\omega t)`

Finally, the equation of the motion of the system is:

`x=(0.088m)\cos(\omega t)`

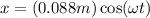
or

`x=(0.088m)\cos(\sqrt{(k)/(m) } t)`