Question

A recent study of 500 American males aged 18-21 found that 237 had 1 ticket in the past year, 112 had 2 tickets in the past year, 17 had 3 tickets in the past year, 5 had 4 tickets in the past year, and 1 had 5 tickets in the past year. The rest of the men did not have any tickets in the past year. What is the expected number of tickets an 18-21-year-old American male will have in one year?

Answer 1

The expected number of tickets is 1.273

Explanation:

Expected Value of a Discrete Probability Distribution

Given a discrete distribution with values

x={x1,x2,x3,...,xn}

And respective probabilities

p={p1,p2,p3,...pn}

The expected value EX of the entire distribution is

`EX=\sum_(i)x_i.p_i`

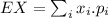
The recent study of American males provides an approximate distribution of probabilities based on the number of tickets they had past year, according to the following data:

237 had 1 ticket

112 had 2 tickets

17 had 3 tickets

5 had 4 tickets

1 had 5 tickets

The total number of tickets is 237+112+17+5+1=372

Taking the number of tickets as the independent variable, then

x={1,2,3,4,5}

Each probability can be found as the relative frequency of the number of tickets as follows:

`\displaystyle p_1=(237)/(372)=0.637`

`\displaystyle p_2=(112)/(372)=0.301`

`\displaystyle p_1=(17)/(372)=0.046`

`\displaystyle p_1=(5)/(372)=0.013`

`\displaystyle p_1=(1)/(372)=0.003`

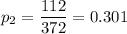
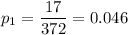
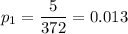
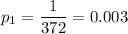
Therefore

p={0.637,0.301,0.046,0.013,0.003}

Compute EX

`EX=1*0.637+2*0.301+3*0.046+4*0.013+5*0.003`

`\boxed{EX=1.273}`

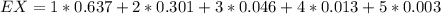
The expected number of tickets is 1.273