Question

Hydroxyapatite, Ca 10 ( PO 4 ) 6 ( OH ) 2 , has a solubility constant of Ksp = 2.34 × 10 − 59 , and dissociates according to Ca 10 ( PO 4 ) 6 ( OH ) 2 ( s ) − ⇀ ↽ − 10 Ca 2 + ( aq ) + 6 PO 3 − 4 ( aq ) + 2 OH − ( aq ) Solid hydroxyapatite is dissolved in water to form a saturated solution. What is the concentration of Ca 2 + in this solution if [ OH − ] is fixed at 3.90 × 10 − 6 M ?

Answer 1

Hydroxyapatite, Ca10(PO4)6(OH)2 , has a solubility constant of Ksp = 2.34×10−59 , and dissociates according to Ca10(PO4)6(OH)2(s)↽−−⇀10Ca2+(aq)+6PO3−4(aq)+2OH−(aq) Solid hydroxyapatite is dissolved in water to form a saturated solution.

Step-by-step explanation:

Answer 2

Answer: The concentration of
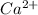`Ca^(2+)` ions in the solution is
`7.81* 10^(-4)M`

Step-by-step explanation:

We are given:

Concentration of hydroxide ion =
`3.90* 10^(-6)M`

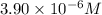
Solubility product is defined as the product of concentration of ions present in a solution each raised to the power its stoichiometric ratio.

The equation for the ionization of the hydroxyapatite is given as:

`Ca_(10)(PO_4)_6(OH)_2(s)\leftrightharpoons 10Ca^(2+)(aq.)+6PO_4^(3-)(aq.)+2OH^-(aq.)`

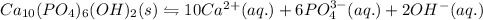
10s 6s
`(3.90* 10^(-6)+2s)`

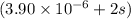
The expression for the solubility product of hydroxyapatite will be:

`K_(sp)=[Ca^(2+)]^10[PO_4^(3-)]^6[OH^-]^2\\\\K_(sp)=(10s)^(10)* (6s)^6* (3.90* 10^(-6)+2s)^2=4.6656* 10^(14)* s^(16)* (3.90* 10^(-6)+2s)^2`

We are given:

`K_(sp)=2.34* 10^(-59)`

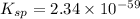
Putting values in above equation, we get:

`2.34* 10^(-59)=4.6656* 10^(14)* s^(16)* (3.90* 10^(-6)+2s)^2\\\\s=7.81* 10^(-5),-7.86* 10^(-5)`

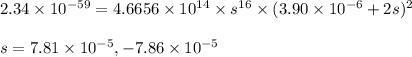
Neglecting the negative value of 'x' because concentration cannot be negative.

So, the concentration of calcium ions in the solution = 10s =
`[10* (7.81* 10^(-5))]=7.81* 10^(-4)M`

Hence, the concentration of
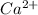`Ca^(2+)` ions in the solution is
`7.81* 10^(-4)M`