Question

I roll a fair die twice and obtain two numbers X1= result of the first roll and X2= result of the second roll. Given that I know X1+X2=7, what is the probability that X1=4 or X2=4?

Answer 1

By definition of conditional probability,

`P(X_1=4\text{ or }X_2=4\mid X_1+X_2=7)=\frac{P((X_1=4\text{ or }X_2=4)\text{ and }X_1+X_2=7)}{P(X_1+X_2=7)}`

`=\frac{P((X_1=4\text{ and }X_1+X_2=7)\text{ or }(X_2=4\text{ and }X_1+X_2=7))}{P(X_1+X_2=7)}`

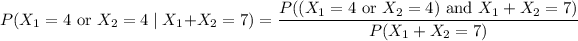
Assuming a standard 6-sided fair die,

• if
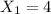  `X_1=4`, then
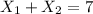  `X_1+X_2=7` means
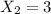  `X_2=3`; otherwise,
• if
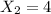  `X_2=4`, then
  `X_1=3`.

Both outcomes are mutually exclusive with probability
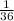`\frac1{36}` each, hence total probability
`\frac2{36}=\frac1{18}`.

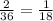Of the 36 possible outcomes, there are 6 ways to sum the integers 1-6 to get 7:

(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)

and so a sum of 7 occurs
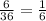`\frac6{36}=\frac16` of the time.

Then the probability we want is

`P(X_1=4\text{ or }X_2=4\mid X_1+X_2=7)=\frac{\frac1{18}}{\frac16}=\frac13`