Question

You walk 45 m to the north. You then turn 160° to your right and walk another 45 m. Finally you go 10 m due west. How far are you from where you originally started?

Answer 1

`R= \sqrt{F^2_(Rx) +F^2_(Ry)}= √((-52.286)^2 +(60.39)^2) = 79.880 m`

And the angle would be:

`\theta= tan^(-1) ((F_(Ry))/(F_(Rx))) =tan^(-1) ((60.39)/(-52.286))= -49.11`

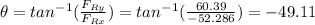
So the final position would be 79.880m and with an angle of
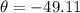`\theta= -49.11` Southwest

Step-by-step explanation:

For this case we can use the method of components to solve this problem. And we have the following info given.

`u_1 = 45m \theta_1 = 90`

`u_2 = 45m \theta_2 = 160`

`u_3 = 10m \theta_3 = 180`

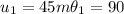
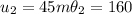
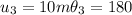
Now we can find the components for each vector like this:

`u_(x_1) = 45m *cos 90 =0 , u_(y_1)= 45m *sin 90 =45m`

`u_(x_2) = 45m *cos 160 =-42.286 , u_(y_2)= 45m *sin 160 =15.39m`

`u_(x_3) = 10m *cos 180 =-10 , u_(y_3)= 10m *sin 180 =0m`

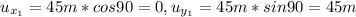
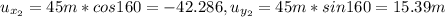
Now we can find the net vectors on x and y:

`F_(Rx)= 0 -42.286 -10= -52.286 m`

`F_(Ry)= 45 +15.39 +0 m = 60.39 m`

And the resultant position would be:

`R= \sqrt{F^2_(Rx) +F^2_(Ry)}= √((-52.286)^2 +(60.39)^2) = 79.880 m`

And the angle would be:

`\theta= tan^(-1) ((F_(Ry))/(F_(Rx))) =tan^(-1) ((60.39)/(-52.286))= -49.11`

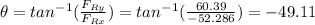
So the final position would be 79.880m and with an angle of
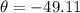`\theta= -49.11` Southwest