Question

A rectangle has a length 6 more than it's width if the width is decreased by 2 and the length decreased by 4 the resulting has an area of 21 square units what is the length of the original rectangle what is ratio of the original rectangle area to the new rectangle area what is the perimeter of the new rectangle

Answer 1

Length of original rectangle: 11 units.

`\frac{\text{Area of original rectangle}}{\text{Area of new rectangle}}=(55)/(21)`

`\text{Perimeter of new rectangle}=20`

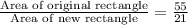
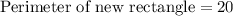
Explanation:

Let x represent width of the original rectangle.

We have been given that a rectangle has a length 6 more than it's width. S the length of the original rectangle would be
`x+6`.

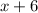We have been given that when the width is decreased by 2 and the length decreased by 4 the resulting has an area of 21 square units.

The width of new rectangle would be
`x-2`.

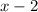The length of new rectangle would be
`x+6-4=x+2`.

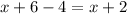The area of new rectangle would be
`(x+2)(x-2)`.

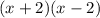Now we will equate area of new rectangle with 21 and solve for x as:

`(x+2)(x-2)=21`

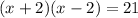
Applying difference of squares, we will get:

`x^2-2^2=21`

`x^2-4=21`

`x^2-4+4=21+4`

`x^2=25`

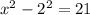
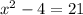
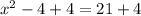
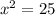
Since width cannot be negative, so we will take positive square root of both sides.

`√(x^2)=√(25)`

`x=5`

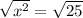
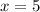
Therefore, the width of original rectangle is 5 units.

Length of the original rectangle would be
`x+6\Rightarrow x+5=11`.

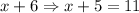Therefore, the length of original rectangle is 11 units.

`\text{Area of original rectangle}=5* 11`

`\text{Area of original rectangle}=55`

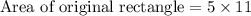
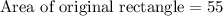
Therefore, area of the original rectangle is 55 square units.

Now we will find ratio of the original rectangle area to the new rectangle area as:

`\frac{\text{Area of original rectangle}}{\text{Area of new rectangle}}=(55)/(21)`

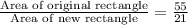
We know that perimeter of rectangle is two times the sum of length and width.

`\text{Perimeter of new rectangle}=2((x+2)+(x-2))`

`\text{Perimeter of new rectangle}=2((5+2)+(5-2))`

`\text{Perimeter of new rectangle}=2(7+3)`

`\text{Perimeter of new rectangle}=2(10)`

`\text{Perimeter of new rectangle}=20`

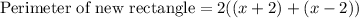
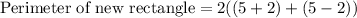
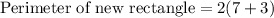
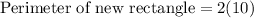
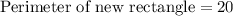
Therefore, the perimeter of the new rectangle is 20 units.