Question

an object moves in simple harmonic motion with amplitude 13 m and period 3 minutes. At time t= 0 minutes, its displacement d from rest is -13 m, and initially it moves in a positive direction.

Answer 1

`x(t) = (13\,m)\cdot \cos \left[(2\pi)/(3)\cdot t \pm \pi\right]`, where t is measure in minutes.

Explanation:

The statement consists in the construction of the motion function for a object experimenting a simple harmonic motion. The expression for simple harmonic motion is:

`x(t) = A\cdot \cos (\omega\cdot t + \phi)`

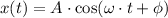
Where:

`A` - Amplitude, in m.

`\omega` - Angular frequency, in rad/s.

`\phi` - Phase angle, in rad.

The angular frequency is:

`\omega = (2\pi)/(T)`

`\omega = (2\pi)/(180\,s)`

`\omega = (\pi)/(90)`

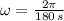
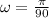
The amplitude of the motion is 13 m and the phase angle is:

`(13\,m)\cdot \cos \phi = -13\,m`

`\cos \phi = -1`

`\phi = \pm\pi`

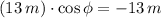
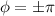
The position function for the object is:

`x(t) = (13\,m)\cdot \cos \left[(2\pi)/(3)\cdot t \pm \pi\right]`, where t is measure in minutes.