Answer:
The train is moving with a speed of 57.6 m/s.
Step-by-step explanation:
Given that,
Distance of observer from the road, d = 40 m (due south)
Velocity of the train, v = 60 m/s (due east)
So,

t is time
Net displacement is given by :
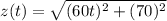
Differentiating above equation wrt t as :
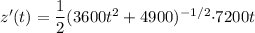
Put t = 4 s
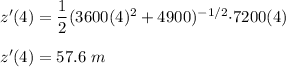
So, the train is moving with a speed of 57.6 m/s.