Question

Find the quotient of these Complex Numbers.


(5-i) / (3+2i)

Answer 1

Let the given complex number

z = x + ix =
`(5-i)/(3+2i)`

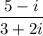
We have to find the standard form of complex number.

Solution:

∴ x + iy =
`(5-i)/(3+2i)`

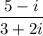
Rationalising numerator part of complex number, we get

x + iy =
`(5-i)/(3+2i)* (3-2i)/(3-2i)`

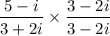
⇒ x + iy =
`((5-i)(3-2i))/(3^2-(2i)^2)`

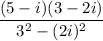
Using the algebraic identity:

(a + b)(a - b) =
`a^(2)` -
`b^(2)`

⇒ x + iy =
`(15-10i-3i+2i^2)/(9-4i^2)`

⇒ x + iy =
`(15-13i+2(-1))/(9-4(-1))` [ ∵
`i^(2) =-1`]

⇒ x + iy =
`(15-2-13i)/(9+4)`

⇒ x + iy =
`(13-13i)/(13)`

⇒ x + iy =
`(13(1-i))/(13)`

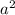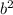
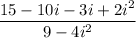
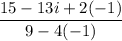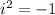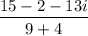
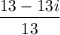
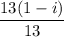
⇒ x + iy = 1 - i

Thus, the given complex number in standard form as "1 - i".