Question

Inclusions are defects in poured metal caused by contaminants. The number of (large) inclusions in cast iron follows a Poisson distribution with a rate of 3.7 per cubic millimetre. What is the volume of material to inspect such that the probability of at least one inclusion is 0.99

Answer 1

The volume needed is 1.245 cubic millimetres.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

The number of (large) inclusions in cast iron follows a Poisson distribution with a rate of 3.7 per cubic millimetre.

This means that
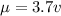`\mu = 3.7v`, in which v is the volume, in cubic millimeters.

What is the volume of material to inspect such that the probability of at least one inclusion is 0.99

Either there are no inclusions, or there is at least one. The sum of these probabilities is decimal 1. So

`P(X = 0) + P(X \geq 1) = 1`

`P(X \geq 1) = 1 - P(X = 0)`

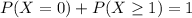
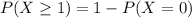
We want
`P(X \geq 1) \geq 0.99`

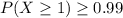
Building the inequality

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-\mu)*\mu^(0))/((0)!) = e^(-\mu)`

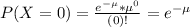
So

`1 - e^(-\mu) \geq 0.99`

`e^(-\mu) = 0.01`

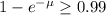
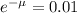
Applying ln to both sides

`\ln{e^(-\mu)} = ln(0.01)`

`-\mu = ln(0.01)`

`\mu = 4.605`

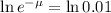
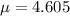
We have that:

Mean rate of 3.7 per cubic millimetre. How many cubic millimetres are 4.605?

4.605/3.7 = 1.245

The volume needed is 1.245 cubic millimetres.