Question

In ΔPQR, the measure of ∠R=90°, the measure of ∠P=52°, and QR = 9.6 feet. Find the length of RP to the nearest tenth of a foot.

Answer 1

7.5

Explanation:

Answer 2

Given:

In ΔPQR, the measure of ∠R=90°, the measure of ∠P=52°, and QR = 9.6 feet.

We need to determine the length of RP.

Length of RP:

The image of the triangle PQR is attached below.

Using the figure, the length of RP can be determined using the trigonometric ratio,

`tan \ \theta=(opp)/(adj)`

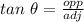
Substituting
`\theta=52^(\circ)`,
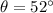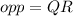`opp=QR` and
`adj=RP`

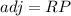
Thus, we get;

`tan \ 52^(\circ)=(QR)/(RP)`

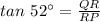
Substituting the values, we get;

`1.2799=(9.6)/(RP)`

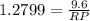
Simplifying, we get;

`RP=(9.6)/(1.2799)`

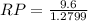
Dividing, we get;

`RP=7.5`

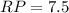
Thus, the length of RP is 7.5 feet.