Question

The diagram shows a 7cm x 6cm rectangle-based pyramid

all the diagonal sides - TA, TB, TC, TD are the length 10 cm

M is the midpoint of the rectangular based.

work out the hight MT. give your answer to 1 decimal place
show your working out

Answer 1

MT = 8.9 cm

Explanation:

In the rectangle ABCD, Angle ABC = 90 degree

In the triangle ABC, Angle B = 90 degree

=> ABC is the right angle triangle

According to the Pythagoras theorem, we have the following equation:

+)
`AB^(2) + BC^(2) = AC^(2)`

⇔
`6^(2) + 7^(2) = AC^(2)`

⇔
`AC^(2) = 36 + 49 = 85`

⇔
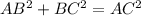
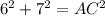
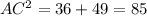
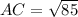`AC = √(85)` cm

In the rectangle ABCD, M is the midpoint, so that it is also the midpoint of line segment AC.

=> AM =
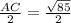`(AC)/(2)=(√(85) )/(2)` cm

TM is the height of the pyramid, so that it is perpendicular to the base ABCD.

As AM belongs to the surface of the rectangle ABCD

=> TM is also perpendicular to AM

=> AMT is the right-angled triangle with Angle AMT = 90 degree

According the Pythagoras theorem, we have the following equation:

`AM^(2) + MT^(2) = AT^(2)`

⇔
`MT^(2) = AT^(2) - AM^(2) = 10^(2) - ((√(85) )/(2) )^(2)`

⇔
`MT^(2) = 100 - (85)/(4) = (315)/(4)`

⇔
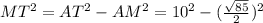
`MT = \sqrt{(315)/(4) } =(3√(35) )/(2)` ≈ 8.9 cm

MT = 8.9 cm