Given:
One secant is x+ 5 and 8
Other secant is x + 1 and 9
To find:
The value of x
Solution:
If two secant segments intersect outside a circle, then the product of one segment and its external segment is equal to the product of other segment and its external segment.
External segment = 8 + x + 5 = x + 13
Another external segment = 9 + x + 1 = x + 10
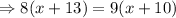
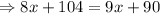
Subtract 90 from both sides.
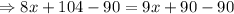
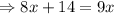
Subtract 8x from both sides.
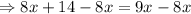
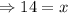
The value of x is 14.