Question

Which of the following correctly displays

`(1)/(2) r - t.`
a, b, c, or d​

Answer 1

b.

Explanation:

In the same way you can think of the addition of real numbers as "go this far on the number line, and then this far," you can of the addition of vectors (typically first encountered as arrows with direction and magnitude) as "travel along this arrow, and then this arrow." Immediately we can eliminate a and c, since there's no clear "first" vector we're travelling along.

We can rewrite
`(1)/(2)\vec{r}-\vec{t}` as
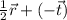`(1)/(2)\vec{r}+(-\vec{t})`, so we can interpret it as "travelling along
`\vec{r}` and then travelling along
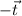`-\vec{t}`". Both b and d represent this scenario, but to see which one makes sense, let's turn back to integer addition for an analogy.

We can interpret the expression 4 + 3 as "starting at 0, moving 4 to the right and then 3 to the right on the number line." Since this is the same as starting at 0 and moving 7 to the right, we say that 4 + 3 = 7. The sum, in other words, takes us from the start of the first movement to the end of the second movement. We start at zero, and end after we've moved right 4 and right 3.

In vectors,
`\vec{a}+\vec{b}` takes us from the start (or tail) of
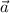`\vec{a}` to the end (or head) of
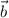`\vec{b}`. Option d represents a trip from head to tail, so we can rule it out, leaving us with the correct option: b, which travels from tail to head.