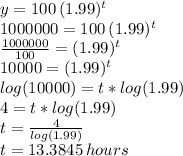Answer:
It would take about 13.4 hours for the bacteria to reach 1,000,000
Explanation:
We use the exponential growth equation the problem provides, to solve for a total of 1,000,000 bacteria.
Recall that "y"in the equation is the number of individuals at time "t"; 100 is the starting number of the initial population, and t represents the elapsed time (in hours). So "t" i our unknown, and we know all the other values. Since "t" is in the exponent, we proceed to: first isolate the exponential expression, and second, to bring that unknown exponent "t" down by the use of logarithms.