Given:
The given equation of line is
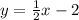
The line passes through the point (-8,1)
We need to determine the equation of the line parallel to the line
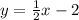
Slope:
Since, the lines are parallel, the slope of the line is given by

Hence, the slope is

Equation of the line:
The equation of the line can be determined using the formula,

Substituting the point (-8,1) and the slope
 in the above formula, we get;
in the above formula, we get;
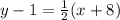
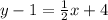

Thus, the equation of the line is

Hence, Option C is the correct answer.