Question

Can anyone help me understand this!!!! please break it down for me to understand!!

answer=462 how do you get it???


​

Answer 1

Given:

`_(11) \bsymbol{C}_(6)`

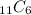
To find:

The value of the expression.

Solution:

Formula for
`_(n){C}_(r)`:

`$ _(n) C_(r)=(n !)/(r !(n-r) !) $`

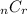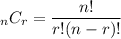
Substitute n = 11 and r = 6.

`$ _(11) C_(6)=(11 !)/(6 !(11-6) !) $`

`$=(11 !)/(6 ! \cdot 5 !)$`

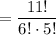
11! = 11 × 10 × 9 × ..... × 2 × 1 also can be written as 11 × 10 × 9 × 8 × 7 × 6!

`$=(11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6!)/(6 ! \cdot 5 !)$`

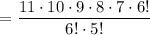
Cancel the common factorials (6!).

`$=(11 \cdot 10 \cdot 9 \cdot 8 \cdot 7)/(5 !)$`

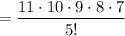
5! = 5 × 4 × 3 × 2 × 1

`$=(11 \cdot 10 \cdot 9 \cdot 8 \cdot 7)/(5 \cdot 4\cdot 3 \cdot 2 \cdot 1)$`

`$=(55440)/(120)`

`=462`

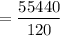
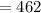
The value of the expression
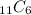`_(11) \bsymbol{C}_(6)` is 462.