Question

Please help i need help

Answer 1

`\mathrm{Slope = (1)/(2)}`

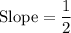
Explanation:

To find the slope of a graph, we use the formula below:

`\mathrm{m =(y\x_(2)-y\x_(1))/(x\y_(2)-x\y_(1))}`

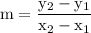
m = slope

(x1, y1) = coordinates of first point in the line

(x2, y2) = coordinates of second point in the line

Step 1: Find any two points on the line

Lets choose: (0, 3) and (2, 4)

Step 2: Put these points into the slope formula

`\mathrm{m =(y\x_(2)-y\x_(1))/(x\y_(2)-x\y_(1))}`

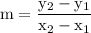
Step 3: Substitute points into formula

`\mathrm{m =(4-3)/(2-0)}`

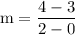
Step 4: Subtract 3 from 4 and 0 from 2

`\mathrm{m =(1)/(2)}`

----------------------------------------------------------------------------------------------------------

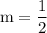
Another way you could easily do this is:

Step 1: Find two ponts on the line

For this problem, let's use (0, 3) and (2, 4)

Step 2: Then from the first point, how much do you need to go up and to the left or right to get to the second point

For this problem, we start on the on the point (0, 4) and go up by 1 and then to the right by 2

Step 3: Then you do rise over run to get the slope

The slope is rise over run:

Rise = 1

Run = 2

So, the slope is 1/2

________________________________________________________
`\mathrm{Answer:(1)/(2)}` ----------------------------------------------------------------------------------------------------------