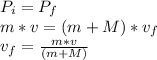Answer:
The final velocity of the melon-arrow system immediately after collision is:
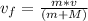
Step-by-step explanation:
We use conservation of momentum to solve this problem.
The initial state consists of an arrow of mass m and speed v , and a static melon that is not moving (velocity = 0)
Therefore, the initial momentum
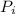 of the system which is the addition of the initial momentum of the arrow (
of the system which is the addition of the initial momentum of the arrow (
 ) plus the initial momentum of the melon (
) plus the initial momentum of the melon (
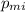 is;
is;
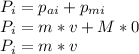
The final system consists of the arrow stack to the melon (total mass "m+M"), travelling at the unknown velocity
 that we need to find. The final momentum of this system is therefore the product of this mass times the unknown velocity:
that we need to find. The final momentum of this system is therefore the product of this mass times the unknown velocity:
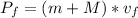
Due to conservation of momentum in this inelastic collision, we set the equation that equals the system's initial momentum to the final momentum, and solve for the unknown velocity: