(a)The power series converges when x = 10: False
(b)The power series converges when x = 3: False
(c)The power series diverges when x = 1: False
(d)The power series diverges when x >= 6: False
The given information tells us that the power series converges when x = -4 and diverges when x = 7. This means that the series converges for all values of x within the interval (-4, 7).
Statement (a):
The power series converges when x = 10. This statement is false. Since the given power series diverges when x = 7, it must also diverge for any value of x within the interval (
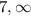 ). Therefore, the series diverges when x = 10.
). Therefore, the series diverges when x = 10.
Statement (b):
The power series converges when x = 3. This statement is false. Since the given power series converges when x = -4, it must also converge for any value of x within the interval (-4, 3). However, the statement does not provide any information about the interval beyond x = 3. Therefore, it is not possible to determine whether the series converges when x = 3.
Statement (c):
The power series diverges when x = 1. This statement is false. Since the given power series converges when x = -4, it must also converge for any value of x within the interval (-4, 1). Therefore, the series converges when x = 1.
Statement (d):
The power series diverges when x ≥ 6. This statement is false . Since the given power series diverges when x = 7 , it must also diverge for any value of x within the interval (7,
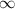 ). However, the statement does not provide any information about the interval between x = 6 and x = 7. Therefore, it is not possible to determine whether the series diverges when x >= 6
). However, the statement does not provide any information about the interval between x = 6 and x = 7. Therefore, it is not possible to determine whether the series diverges when x >= 6
Complete question below:
Suppose that the power series,
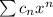 , converges when x = -4 and diverges when x = 7. Determine whether each statement is true, false, or not possible to determine.
, converges when x = -4 and diverges when x = 7. Determine whether each statement is true, false, or not possible to determine.
(a) The power series converges when x = 10.
(b) The power series converges when x = 3.
(c) The power series diverges when x = 1.
(d) The power series diverges when x = 6.