answers
velocity = 7 m/s
tension = 7.644 N
set up equation for velocity
because energy is conserved, the change in potential energy as the potato drops is the same as the change in kinetic energy
U = K
mgh = m
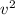 /2
/2
gh =
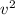 /2
/2
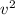 = 2gh
= 2gh
v =

values
g = 9.8 m/s^2
h = 2.5 m (change in vertical distance)
plug in values and solve
v =

v =

v = 7 m/s
set up equation for tension
at the lowest point, tension (directly upward) acts in the opposite direction of weight (directly downwards) so
∑F = T - mg
since the potato is in circular motion, the net force is equal to centripetal force
∑F = m
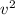 /r
/r
∑F = T - mg = m
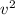 /r
/r
T - mg = m
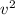 /r
/r
T = mg + m
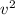 /r
/r
T =
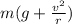
values
m = 0.26 kg
g = 9.8 m/s^2
v = 7 m/s
r = 2.5m
plug in values and solve
T =
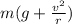
T =
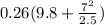
T = 7.644 N