Answer:
The speed of the current is 7 miles per hour.
Explanation:
Let x represent speed of the current.
We have been given that a motorboat maintained a constant speed of 11 miles per hour relative to the water in going 18 miles upstream and then returning.
The speed of motorboat while going upstream would be
 .
.
The speed of motorboat while going downstream would be
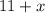 .
.
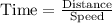
Time taken while going upstream would be
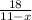 .
.
Time taken while going downstream would be
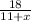 .
.
Now we will compare sum of both times with total time 5.5 hours and solve for x as:
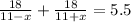
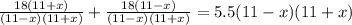
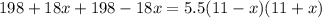
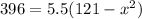
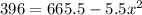
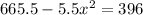
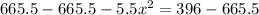
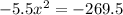

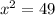
Take positive square root of both sides:
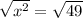
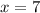
Therefore, the speed of the current is 7 miles per hour.