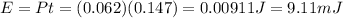Question

A 129 129 ‑turn circular coil of radius 2.21 cm 2.21 cm and negligible resistance is immersed in a uniform magnetic field that is perpendicular to the plane of the coil. The coil is connected to a 11.7 Ω 11.7 Ω resistor to create a closed circuit. During a time interval of 0.147 s, 0.147 s, the magnetic field strength decreases uniformly from 0.637 T 0.637 T to zero. Find the energy, in millijoules, that is dissipated in the resistor during this time interval.

Answer 1

9.11 mJ

Step-by-step explanation:

Electromagnetic induction occurs when there is a change in magnetic flux linkage through a coil, and an electromotive force is induced in the coil, according to Faraday-Newmann-Lenz law:

`\epsilon = - (N\Delta \Phi)/(\Delta t)`

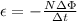
where

N is the number of turns in the coil

`\Delta \Phi` is the change in magnetic flux through the coil

`\Delta t` is the time interval

The change in magnetic flux can be rewritten as

`\Delta \Phi = A\Delta B`

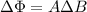
where

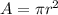`A=\pi r^2` is the area of the coil

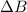`\Delta B` is the variation of the strength of the magnetic field

So the equation becomes

`\epsilon=-(N\pi r^2 \Delta B)/(\Delta t)`

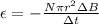
here we have:

N = 129 turns

`r=2.21 cm = 0.0221 m`

`\Delta B=0-0.637 = -0.637 T`

`\Delta t = 0.147 s`

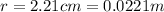
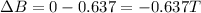
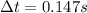
So the induced emf is

`\epsilon=-((129)\pi (0.0221)^2(-0.637))/(0.147)=0.857 V`

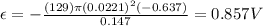
We know that the resistance of the coil is

`R=11.7 \Omega`

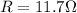
so the current in the circuit is given by Ohm's law:

`I=(\epsilon)/(R)=(0.857)/(11.7)=0.073 A`

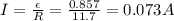
And the power dissipated through the resistor is:

`P=I^2 R=(0.073)^2(11.7)=0.062 W`

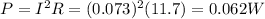
And finally, the energy dissipated in the resistor in this time interval is:

`E=Pt=(0.062)(0.147)=0.00911 J = 9.11 mJ`