Question

Ask Your Teacher A beam of light is incident from air on the surface of a liquid. If the angle of incidence is 33.5° and the angle of refraction is 19.3°, find the critical angle for the liquid when surrounded by air.

Answer 1

The critical angle for the liquid when surrounded by air is 30 degrees.

Step-by-step explanation:

Given that,

The angle of incidence is 33.5° and the angle of refraction is 19.3°. Firstly, we can find the refractive index of the liquid. It can be calculated using Snell's law as :

`n=(\sin i)/(\sin r)\\\\n=(\sin (33.5))/(\sin (19.3))\\\\n=2`

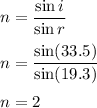
The critical angle is given by :

`\theta_c=\sin^(-1)((n_1)/(n_2))`

Here,
`n_1` is refractive index of air and
`n_2` is refractive index of liquid.

`\theta_c=\sin^(-1)((1)/(2))\\\\\theta_c=30^(\circ)`

So, the critical angle for the liquid when surrounded by air is 30 degrees.