Answer:
a. Wgra=786.09J
b. 1.28m
Step-by-step explanation:
The change in the potential energy is the work done by the gravitational force.
For this problem you have to take into account that the total work done is given by the change in the kinetic energy
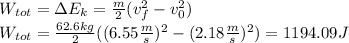
Furthermore the total work is the contribution of the work done by the skater, the gravitational force and the friction

(a) by separating Wfric you have
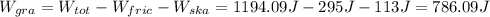
(b) It is only necessary to use the expression for the work done by gravitational force

HOPE THIS HELPS!!