Length of original rectangle is : x+6 = 5+6 = 11 units
ratio of the original rectangle area to the new rectangle area:
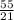
perimeter of the new rectangle : 2(x+2+x-2) = 4x = 4(5) = 20 units
Explanation:
Here we have , A rectangle has a length 6 more than it’s width if the width is decreased by 2 and the length decreased by 4 the resulting has an area of 21 square units what is the length of the original rectangle . We need to find what is ratio of the original rectangle area to the new rectangle area what is the perimeter of the new rectangle . Let's find out:
Initial parameters of rectangle are : Length = x+6 , width = x
width is decreased by 2 and the length decreased by 4 :
Length = x+6-4 = x+2 , width = x -2 , So area is :
⇒
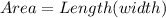
⇒
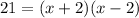
⇒
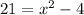
⇒
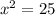
⇒
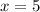
So , Length of original rectangle is : x+6 = 5+6 = 11 units
ratio of the original rectangle area to the new rectangle area:
⇒
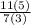
⇒
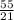
perimeter of the new rectangle : 2(x+2+x-2) = 4x = 4(5) = 20 units