Question

Assume that the average age at which students graduate high school is 17.6. Exum (2002) asked 84 male students at a large Mid-Atlantic University the age at which they had their first alcoholic drink. On average, these 84 students had their first alcoholic drink at 16.54 years of age (standard deviation

Answer 1

The null hypothesis is rejected. It can be concluded that the average age of first drink is less that 17.6 years.

Explanation:

A one-sample z-test can be used to determine whether the average age at which students graduate high school and had their first drink is less than 17.6 years.

The hypothesis can be defined as:

H₀: The average age of first drink is 17.6 years, i.e. μ = 17.6.

Hₐ: The average age of first drink is less that 17.6 years, i.e. μ < 17.6.

The information provided is:

`n=84\\\bar x=16.54\\\sigma=2.03\\\alpha =0.05`

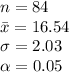
We are using the z-test because the population standard deviation is known and the sample size is quite large, i.e. n = 84 > 30.

Compute the test statistic value as follows:

`z=(\bar x-\mu)/(\sigma/√(n))=(16.54-17.6)/(2.03/√(84))=-4.79`

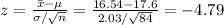
The test statistic value is -4.79.

Decision rule:

If the p-value of the test is less than the significance level (α) then the null hypothesis will be rejected and vice-versa.

Compute the p-value as follows:

`p-value=P(Z<-4.79)\\=1-P(Z<4.79)\\=1-(\approx1)\\=0`

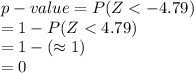
*Use a z-table for the probability.

The p-value of the test is 0.

The p-value = 0 < α = 0.05.

Thus, the null hypothesis will be rejected at 5% level of significance.

Conclusion:

As the null hypothesis is rejected it can be concluded that the average age of first drink is less that 17.6 years.