Answer:
Each factory should supply 100 units
x = 100 units
y = 100 units
Explanation:
Since the total production must be 200 units, then x + y = 200.
The cost function can be rewritten as a function of 'x' as follows:
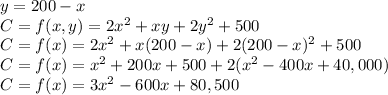
The value of 'x' for which the derivate of the cost function is zero, is the production level that minimizes cost:
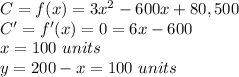
In order to minimize production costs, each factory should supply 100 units