Answer:
The resistance is 24.9 Ω
Step-by-step explanation:
The resistivity is equal to:
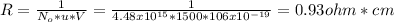
The area is:
A = 60 * 60 = 3600 um² = 0.36x10⁻⁴cm²
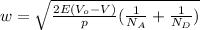
If NA is greater, then, the term 1/NA can be neglected, thus the equation:
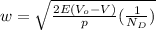
Where
V = 0.44 V
E = 11.68*8.85x10¹⁴ f/cm

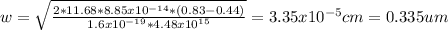
The length is:
L = 10 - 0.335 = 9.665 um
The resistance is:
