Question

A liquid with a density of 900kg/m 3 is stored in a pressurized, closed storage tank. The tank is cylindrical with a 10m diameter. The absolute pressure in the tank above the liquid is 200kPa. What is the initial velocity of a fluid jet when a 5cm diameter orifice is opened at point A?

Answer 1

18.62 m/s

Step-by-step explanation:

Given that:

A liquid with a density of 900 kg/m 3 is stored in a pressurized, closed storage tank.

Diameter of the tank = 10 m

The absolute pressure in the tank above the liquid is 200 kPa = 200, 000 Pa

At pressure of 200 kPa ; the final velocity = 0

Atmospheric pressure at 5cm = 101325 Pa

We are to calculate the initial velocity of a fluid jet when a 5cm diameter orifice is opened at point A?

By using Bernoulli's theorem between the shaded portion in the diagram;

we have:

`Pa \ + \ (1)/(2) \ \delta \ v^2_1 \ + \ \delta gy_1 = P + \delta gy_2`

`(1)/(2) \ \delta \ v^2_1 \ = P + \delta gy_2 - \ \delta gy_1 - Pa`

`(1)/(2) \ \delta \ v^2_1 \ = \delta g(y_2 -y_1 )+ ( P - Pa )`

`v_1 \ = \sqrt{ \frac {2 \ \delta g(y_2 -y_1 )+ 2 ( P - Pa )}{\delta}}`

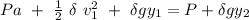
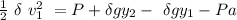
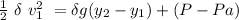
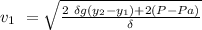
where;

Pa = atmospheric pressure = 101325 Pa

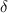`\delta` = density of liquid = 900 kg/m³

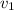`v_1` = initial velocity = ???

g = 9.8 m/s²

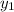`y_1` = height of the hole from the buttom

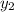`y_2` = height of the liquid surface from the button

`v_1 \ = \sqrt{ \frac {2*900*9.8(7 - 0.5 )+ 2 ( 200,000 - 101325 )}{900}}`

`v_1 = 18.62 \ m/s`

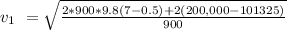
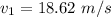
Thus, the initial velocity of the fluid jet = 18.62 m/s